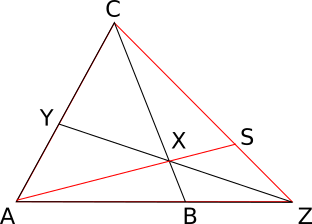
解答例 　

チェバの定理を使う。

線分 $CZ$ と線分 $AX$ の延長の交点を $S$ とする。 チェバの定理により、 $$\frac{CY}{YA}\cdot\frac{AB}{BZ}\cdot\frac{ZS}{SC} = 1$$

ところで、

$\triangle XAB = \frac{BX}{XC} \times \triangle XCA$

$\triangle XAZ = \frac{ZS}{SC} \times \triangle XCA$

ここで、$\triangle XAB$ は三角形 $XAB$ の面積のことである。

$\triangle XAB : \triangle XAZ = AB : AZ $ より、$\frac{ZS}{SC} = \frac{BX}{XC}\cdot\frac{AZ}{AB}$。

よって題意の関係式が得られる。