教材アーカイブス/算数・数学/問題/幾何/三角形/フェルマーの問題/解答例
解答例
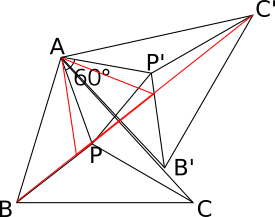
$\triangle ABC$ を頂点 $A$ を中心に $60^{\circ}$ だけ回転させる。
点 $B$ が移った点を $B^{\prime}$ とする。 他の点についても移った先の点には $^{\prime}$ を付けて表す。
$\triangle APP^{\prime}$ は正三角形。 だから、 $$PA + PB + PC = BP + PP^{\prime} + P^{\prime}C^{\prime}$$
点 $P$ が題意を満たすには折れ線 $BPP^{\prime}C^{\prime}$ が線分 $BC^{\prime}$ となるように点 $P$ をとれば良い。
すなわち、点 $P$ はどの二つの頂点も $120^{\circ}$ で見込む場所におくとよい。
この点 $P$ のことをフェルマー点とよぶ。