- еұҘжӯҙдёҖиҰ§
- е·®еҲҶ гӮ’иЎЁзӨә
- зҸҫеңЁгҒЁгҒ®е·®еҲҶ гӮ’иЎЁзӨә
- гӮҪгғјгӮ№ гӮ’иЎЁзӨә
- ж•ҷжқҗгӮўгғјгӮ«гӮӨгғ–гӮ№/з®—ж•°гғ»ж•°еӯҰ/е•ҸйЎҢ/е№ҫдҪ•/еҜҫз§°жҖ§/еҸҚи»ў004 гҒёиЎҢгҒҸгҖӮ
- 1 (2024-06-14 (йҮ‘) 18:22:48)
е•ҸйЎҢ†
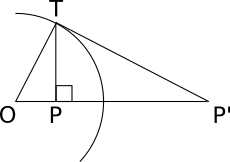
еҶҶ $O$ гҒ®е‘ЁдёҠгҒ«1зӮ№ $T$ гӮ’гҒЁгӮӢгҖӮ $T$ гҒ§гҒ®жҺҘз·ҡгҒЁеҶҶгҒ®дёӯеҝғ $O$ гӮ’йҖҡгӮӢзӣҙз·ҡгҒЁгҒ®дәӨзӮ№гӮ’ $P^{\prime}$гҖҒ $T$ гҒӢгӮүгҒ“гҒ®зӣҙз·ҡгҒ«дёӢгӮҚгҒ—гҒҹеһӮз·ҡгҒ®и¶ігӮ’ $P$ гҒЁгҒҷгӮӢгҖӮ
гҒ“гҒ®гҒЁгҒҚгҖҒ $$OP \cdot OP^\prime = OT^2$$ гҒ§гҒӮгӮӢгҖӮ зӨәгҒӣгҖӮ
гҒ“гӮҢгҒҜеҸҚи»ўгӮ’дҪңеӣігҒҷгӮӢж–№жі•гҒ§гҒҷгҖӮ
see.гҒ“гҒЎгӮү
Tag: ж•ҷжқҗ з®—ж•° ж•°еӯҰ е•ҸйЎҢ е№ҫдҪ•еӯҰ еӣіеҪў еҜҫз§°жҖ§ еҸҚи»ў дёӯеӯҰ й«ҳж Ў