証明例†

ヒント程度で...

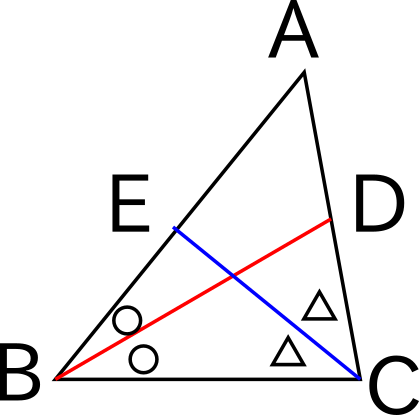
まず一般の三角形について図を書いておきましょう。

A1.png

2つの角の二等分線にはそれぞれ色を付けておきましょう。赤と青。

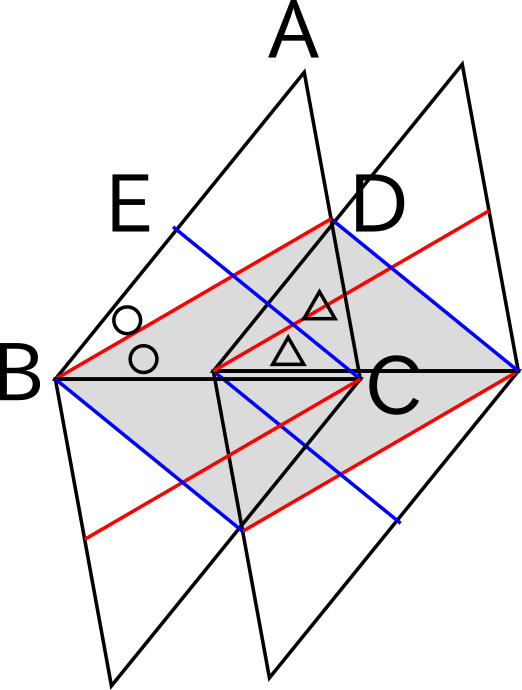
この三角形に合同な三角形を(赤線と青線つきで)さらに3つ用意して、うち2つは$180^{\circ}$回転させておきましょう。

これらを組み合わせて、赤線と青線を辺にもつ平行四辺形を作ります(次の図のグレー)。

A2.png

もし$BD = CE$、つまり赤辺と青辺の長さが等しければ平行四辺形は菱形。 このとき、あきらかに角〇と角△は等しい。

つまり、

$\angle ABC = \angle ACB$

したがって、

$\triangle ABC$ は二等辺三角形になるから

$AB = AC$

えらい直感的。