教材アーカイブス/算数・数学/問題/離散/ラムゼーの定理/解答例
解答例
2人が「知り合いである」なら2人を結ぶ線分を赤色、2人が「知り合いでない」なら2人を結ぶ線分を青色に塗ることを考えよう。 この時、ある3人が作る3角形で3辺すべてが同じ色(赤色あるいは青色のどちらか一方の色)のものが存在することを示せばよい。
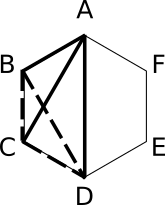
6人を正6角形の頂点に配置し、適当に$A$、$B$、...、$F$ と名付けよう。
1つの頂点からは5本の線分がひける。 これらのうち少なくとも3本は同じ色である。
そこでいま、頂点 $A$ から3本青色の線が引けたとしよう。 相手は $B$、$C$、$D$ としておく(実線)。
次に3角形 $BCD$ (破線)に着目すると、3辺とも同じ色か、2辺が同じ色で残り1辺は異なる色、のどちらかに塗り分けられる。 だから、3角形 $BCD$ の3辺のうち少なくとも1辺が青色なら3辺とも青色の3角形が存在することがわかる( $A$ も入れて考えるからね)。
また3角形 $BCD$ の3辺すべてが赤色なら、やはり3辺とも同じ色の3角形(3角形 $BCD$ そのもの)が存在する。
関係図を書いて考えるとよいですね。