教材アーカイブス/算数・数学/問題/関数/関数とグラフ/2次関数001
問題
2次関数をフリーハンドで書くときに気を付けることを記す。
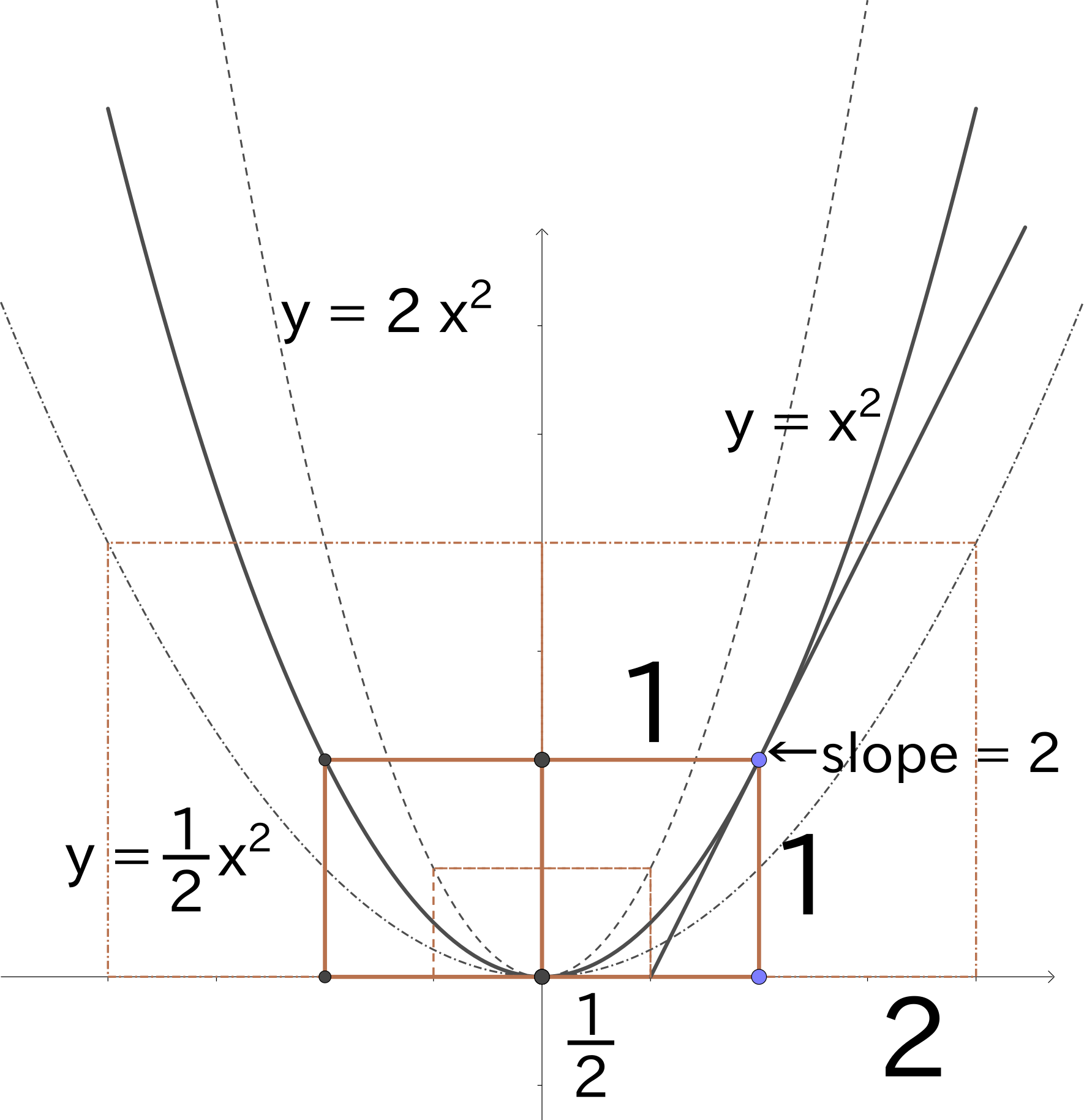
まず $$y = x^2$$ の書き方を説明しよう。
- x軸とy軸を書いた後、1辺の長さが1の正方形を2つ隣り合わせに書く。
- どちらも頂点の1つを原点に置き、1つは第1象限にもう1つは第4象限に書く
- 3ヶ所に目安となる線を引く
- 原点ではx軸に重なる(x軸が接線になる)ように、下に凸であることがわかるようにほんの少しの長さの曲線を書いておく
- 点$(1,1)$を通る傾き$2$の線をほんの少し書いておく。線対称になる点$(-1,1)$では傾き$-2$の線を書いておく
- 目安の線を結び延長する。末広がりになるように。
以上の通りにやって基本の書き方を覚えたら、次は $$y = \frac{1}{a}x^2$$
この場合は、長さ$a$の正方形を考えればよい。 つまりは、基本関数$y = x^2$の拡大相似である[*1]。上の傾き$\pm 2$の線はここでも同じ。
(図は$a = 2$と$a = \frac{1}{2}$の例)
では、さまざまな2次関数を書いて練習しよう。