教材アーカイブス/算数・数学/問題/関数/関数とグラフ/001/解答例
解答例
ここでは、グラフを書いて示す。
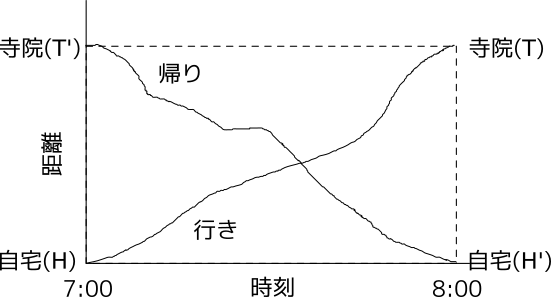
行きの経路上にある自宅を $H$、寺院を $T$ とする。同じく、帰りの自宅を $H'$、寺院を $T'$ とする。 図のように縦軸を自宅から寺院までの「距離」、横軸を「時刻」とすると、行きの経路は $H$ から $T$ を結ぶ一本の曲線 $H - T$ で表せる。 これは四角形 $HH'TT'$ を2つの領域に分ける。 帰りは同様に $T'$ から $H'$ への曲線 $T' - H'$ になるが、両端の点 $T'$ と $H'$ は曲線 $H - T$ で隔てられた異なる領域に属する。 だから帰りの曲線 $T' - H'$ は必ず行きの曲線 $H - T$ と交わる。 その交点が題意の点である。 なお、交点が複数あっても構わない。
変な曲線を考える必要はないから、素直に連続曲線を考えればよいでしょう(そもそも人の運動ですから)。 その形はとくに定まっていない、ということもよいですね(歩いたり走ったり休んだり)。
また「存在」証明ですから、目的のものがあればよいのです。 具体例をだすとか、作り方を示すとかすればよいのです。
この問題は物理の問題としても、運動とグラフについてのよい頭の訓練だと思います。