教材アーカイブス/算数・数学/問題/幾何/2次曲線/004/解答例
解答例
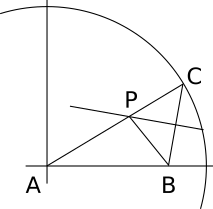
楕円の定義から作図したものをもう一度示す。
この焦点 $A$ が無限に遠くに飛んでいってしまったものを考える(上図では左方に)。 直線 $AP$ は直線 $AB$ に平行になる。
さて、点 $C$ が乗る円周の中心 $A$ が無限遠方にあるのだから、円周は直線になる(図)。 この直線を $m$ とする。直線 $AB$ に垂直。
楕円のとき見たように、点 $C$ は接線を対称軸にして焦点を移した像である。 したがって、 $$BP = CP$$
この直線 $m$ のことを準線と呼ぶ。 放物線はこうして得られる点 $P$ の軌跡のことである。
ここで示した準線を使った仕方で放物線を定義することもある(準線を使うほうが普通かな)。
2次曲線のうちの一つ、放物線を準線を使って表す方法を示した。 同じようにして楕円、双曲線を準線を使って表す方法があっても良い。 さあ、どうしよう?