教材アーカイブス/算数・数学/問題/幾何/対称性/反転001
反転とは
対称操作の一つに鏡映(線対称)がある。これは与えられた直線を対称軸として折り返すものであった。see. 問題
これに対して反転とは、対称軸として直線の代わりに円(反転円と呼ぶ)を用いた、鏡映のような対称操作である。
ちなみに鏡映を半径無限大の反転円を用いた反転と言ってもよいだろう。
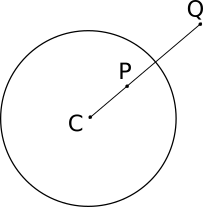
図のように反転円 $C$ が与えられているとき、点 $P$ は反転操作で点 $Q$ に移る。もちろん鏡映のように逆もある。
このとき、円の半径を $k$ とすると、点とその反転像の間には次の関係がある。
$$CP \cdot CQ = k^2$$
問題
反転円は、反転によりその形を変えない(すなわち不変)。 また反転円の中心 $C$ を通る任意の直線も不変である。
示せ。