解答例†

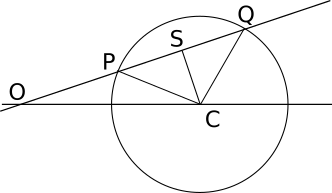
円の半径を $r$ 、中心 $C$から直線に下ろした垂線の足を $S$ とする(図)。

$OP = OS - PS$、$OQ = OS + PS$ だから、 $$OP \cdot OQ = OS^2 - PS^2$$

三平方の定理から $OS^2 = OC^2 - CS^2$、また$CP^2 = CS^2 + PS^2 = r^2$ より $$OP \cdot OQ = OC^2 - r^2$$

円 $C$ と点 $O$ が与えられているので、この値は一定。

この結果を用いると、

• 方べきの定理
  see. 問題

• もう一つ
  see. 問題