教材アーカイブス/算数・数学/問題/幾何/円・楕円/アポロニウスの円/解答例1
解答例
$AP : BP = \mu : 1$ ($\mu > 1$) とする。
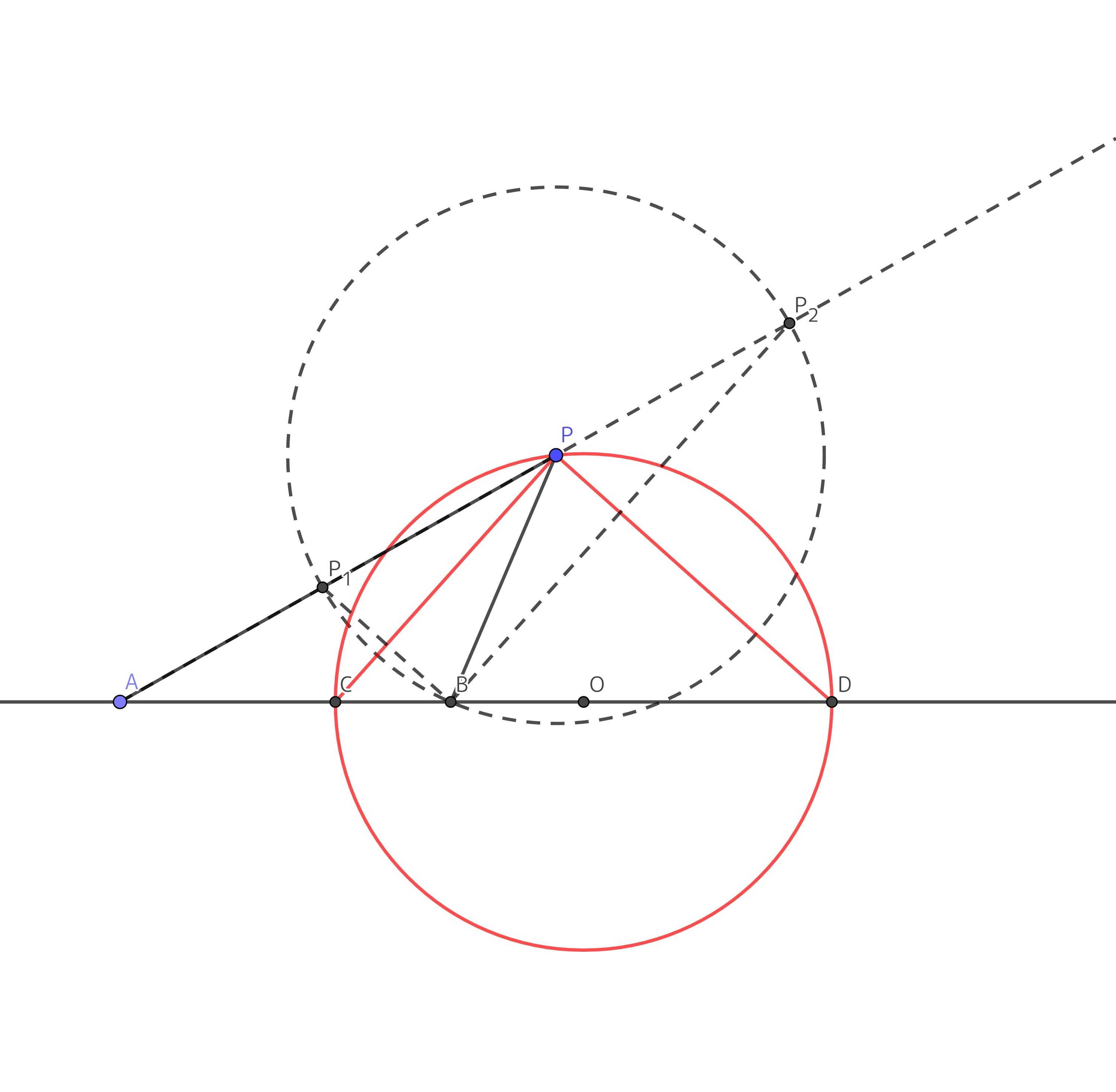
角$APB$の内角および外角の2等分線をひく。 これらの直線と直線$AB$との交点をそれぞれ、点 $C$ および 点 $D$ とする(図)。
これらの2点を直径の両端とする円が求める軌跡である。
以下、そのことを示す。
点 $P$ を中心として半径 $BP$ の円を書き、この円と直線 $AP$ との交点を $P_{1}$、$P_{2}$ とおく。 すると、$PC \parallel P_{2}B$、$PD \parallel P_{1}B$ であることがわかる。
$\triangle APC$ ∽ $\triangle AP_{2}B$だから、 $$AC : AB = \mu : \mu + 1$$ 同様に、 $$AB : AD = \mu - 1 : \mu$$ よって、2点 $C$、$D$ は点 $P$ の位置によらず、定点である。
各点の定め方から、$\angle CPD$ は直角だから、点 $P$ は2点 $C$、$D$ を直径の両端とする円周上にあることがわかる。 この円の中心 $O$ は点 $A$ から $AO = \frac{\mu^2}{\mu^2 - 1}\times AB$ の位置にあり、半径は $\frac{\mu}{\mu^2 - 1}\times AB$ である。
比の話だから相似な三角形が登場するかもしれない、と期待しつつ考えてみるとよいでしょう。
なお、空間内であれば球になりますね。
さて、上によって得られた円、アポロニウスの円の半径を $k = \frac{\mu}{\mu^2 - 1} \times AB$ としよう。 $OB = \frac{1}{\mu^2 - 1} \times AB$ だから、 $$OA \cdot OB = ( \frac{\mu^2}{\mu^2 - 1}\times AB ) \times ( \frac{1}{\mu^2 - 1} \times AB ) = k^2$$ つまり、もともとの2点 $A$ と $B$ はアポロニウスの円による反転で結びつけられる。
もうひとつ。
$OB / OP = OP / OA$ だから、$\triangle OPB$ ∽ $\triangle OAP$ であることもわかる。