教材アーカイブス/算数・数学/問題/幾何/三角形/5心001/解答例
証明例
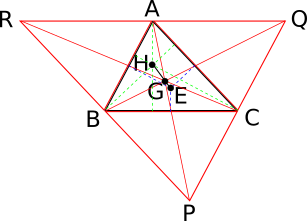
$\triangle ABC$ の各頂点に、それを通る対辺に平行な直線を引く。 これら3本の直線は$\triangle PQR$ を作る(図)。
二つの三角形の重心は一致する。 実際、$\triangle ABC$ と $\triangle PQR$ の対応する頂点を結んだ直線は1点で交わり、その点は明らかにふたつの三角形の重心であることがわかる。 これを $G$ とする。
$G$ はふたつの三角形の相似(拡大)および回転の中心である。 これもまた図を見ればわかることだが、$\triangle ABC$ を$G$ を中心に $180^{\circ}$ 回転させたのち、2倍に拡大してやると $\triangle PQR$ を得ることができる。
このことを利用すれば、$\triangle ABC$ の垂心 $H$ から外心 $E$ を得ることができる。 実際、$\triangle ABC$ の垂心は$\triangle PQR$ の外心でもあるから。
したがって、$\triangle ABC$ の垂心 $H$ と外心 $E$ を結ぶ直線上に重心 $G$ があることがわかる。
この直線のことをオイラー線とよぶ。