教材アーカイブス/算数・数学/問題/幾何/三角形/シュタイナー・レームスの定理/解答例5
証明例
これもヒント程度で...
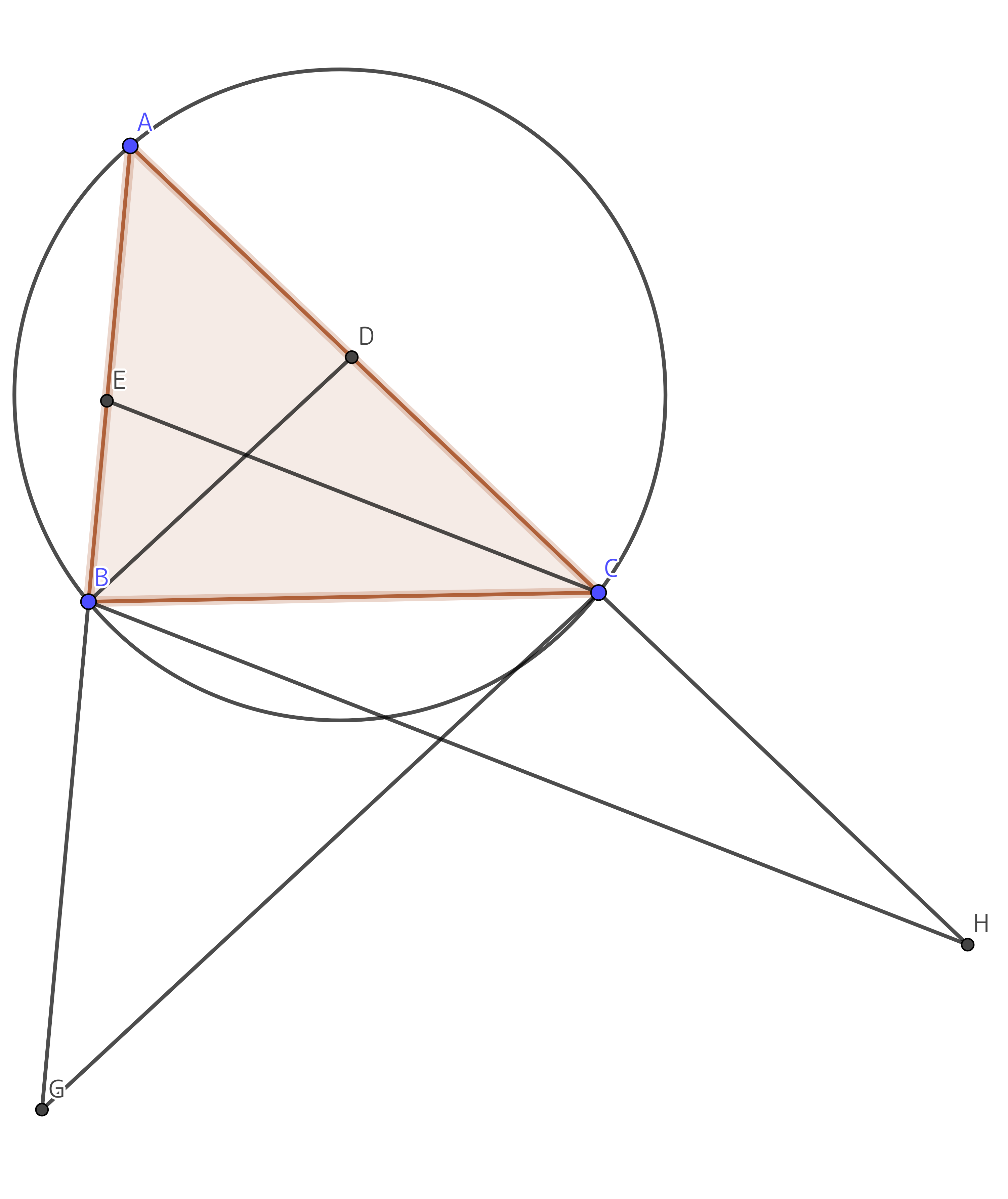
線分$BC$と角$A$の大きさは固定して考えましょう。
すると、点$A$は三角形$ABC$の外接円の周上にある。
点$C$を通って、直線$BD$に平行な直線と直線$AB$との交点を点$G$としましょう。 同様に、点$B$を通って、直線$CE$に平行な直線と直線$AC$との交点を点$H$としましょう。
すると、線分$BD$の長さは、 $$BD = 2 BC \cos(\frac{\angle B}{2}) \times \frac{AB}{AB+BC}$$
同様に、線分$CE$の長さは、 $$CE = 2 BC \cos(\frac{\angle C}{2}) \times \frac{AC}{AC+BC}$$
点$A$を動かしてみましょう。
$\angle B > \angle C$ のときは、$AB < AC$ で、$$BD<CE$$
もちろん、$\angle B = \angle C$ のときは、$AB = AC$となるから、$$BD = CE$$
これも直感的。