教材アーカイブス/算数・数学/問題/幾何/三角形/シュタイナー・レームスの定理/解答例3
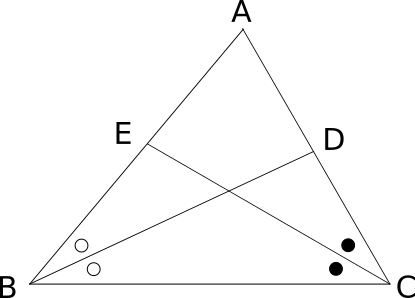
証明例
頂角の2等分線が対辺をどのように分割するか、 こちら (>>) をつかってみるか。
まず、$AD : DC = AB : BC$ 。
すると、$AD = \frac{AB \times AC}{BC + AB}$ 。
同じく、
$AE = \frac{AB \times AC}{BC + AC}$ 。
だから、$AE = AD \iff AB = AC$。
したがって、$AE = AD$ なら、2つの三角形 $\triangle ABD$ と $\triangle ACE$ は合同 (2辺狭角)で
$BD = CE$
$AE \neq AD$ なら $\triangle ABD$ と $\triangle ACE$ は合同ではないので $BD \neq CE$。
結局、$BD = CE$ なら $AB = AC$。