- еұҘжӯҙдёҖиҰ§
- е·®еҲҶ гӮ’иЎЁзӨә
- зҸҫеңЁгҒЁгҒ®е·®еҲҶ гӮ’иЎЁзӨә
- гӮҪгғјгӮ№ гӮ’иЎЁзӨә
- ж•ҷжқҗгӮўгғјгӮ«гӮӨгғ–гӮ№/з®—ж•°гғ»ж•°еӯҰ/е•ҸйЎҢ/е№ҫдҪ•/еҶҶгғ»жҘ•еҶҶ/еҶҶ002/и§Јзӯ”дҫӢ гҒёиЎҢгҒҸгҖӮ
- 1 (2024-06-14 (йҮ‘) 18:22:48)
и§Јзӯ”дҫӢ†
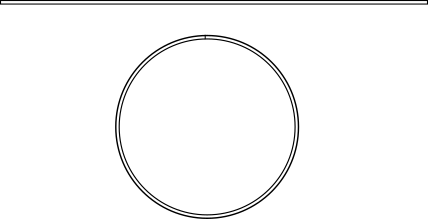
еҚҠеҫ„ $r$ гҒ®еҶҶгҒ®еҶҶе‘Ё(еӨ–зёҒ)гҒ«жІҝгҒЈгҒҰйқһеёёгҒ«зҙ°гҒ„гғ’гғў(е№… $\Delta r$)гӮ’гҒҚгҒЈгҒЎгӮҠ1е‘ЁеҲҶгҒ гҒ‘е·»гҒҸгҖӮ гғ’гғўгҒ®й•·гҒ•гӮ’ $L$ гҒЁгҒҷгӮӢгҖӮ
гҒ“гҒ®зҠ¶ж…ӢгҒ§еҶҶгҒ®йқўз©ҚгӮ’иҖғгҒҲгӮӢгҖӮ е…ғгҒ®еҶҶгҒ®йқўз©Қ $S$ гҒҜ $S = \pi r^2$ гҒ§гҒӮгӮӢгҖӮ гғ’гғўгӮ’е·»гҒ„гҒҹгҒ“гҒЁгҒ«гӮҲгӮҠйқўз©ҚгҒҜеў—гҒҲгҒҰгҖҒ$S' = \pi ( r + \Delta r )^2$ гҒ«гҒӘгӮӢгҖӮ
йқўз©ҚгҒҢеў—гҒҲгҒҹеҲҶгҒҜиҝҪеҠ гҒ—гҒҹгғ’гғўгҒ®еҲҶгҒ гҒӢгӮүгҖҒгғ’гғўгҒ«гӮҲгӮӢйқўз©ҚгҒ®еў—еҠ еҲҶгҒҜ $S' - S = L \Delta r $гҖӮ
гҒЁгҒ“гӮҚгҒ§гҖҒ
$S' - S = \pi ( r + \Delta r )^2 - \pi r^2 = 2 \pi r \times \Delta r + \pi ( \Delta r )^2$
е№… $\Delta r$ гҒҜ $r$ гҒ«жҜ”гҒ№гҒҰеҚҒеҲҶгҒ«зҙ°гҒ„гҒ“гҒЁгҒӢгӮүгҖҒ第2й …гҒ® $\Delta r ^2$ гӮ’з„ЎиҰ–гҒ—гҒҰ
$ L = 2 \pi r $