証明例 　

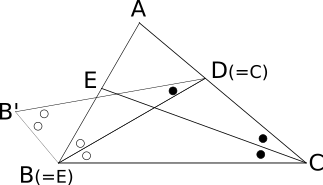
$\triangle EBC$ と $\triangle DBC$ に着目する。 いま $BD = CE$ であるから、$\triangle EBC$ を動かし辺 $EC$ を $\triangle DBC$ の辺 $BD$ に重ねることができる(図)。 重ねた後の $\triangle EBC$ を $\triangle BB'D$ と表そう。

四角形 $B'BCD$ について考える。

$\angle B'BC = \angle B'BD + \angle DBC = \pi - \frac{1}{2}\angle B - \frac{1}{2}\angle C$。

また、 $\angle B'DC = \angle B'DB + \angle BDC = \pi - \frac{1}{2}\angle B - \frac{1}{2}\angle C$。

$\angle B'BC = \angle B'DC$ だから$\angle B = \angle C$ なら、$\angle BEC = \angle BDC $。

このとき四角形 $B'BCD$ は菱形であることがわかるから、$B'B(=BE) = CD$。

つぎに $\triangle AEC$ と $\triangle ADB$ に着目する。 これまでに求めたことから、これら2つの3角形は合同。 だから $AE = AD$。

したがって、 $$AB = AE + EB = AD + DC =AC$$

---

[PS.]この解答なら中学生レベルになりますかね。 でも図形を切り貼りするのは発想力が要りますから、やはり難しい問題と言えるでしょう。

あ?! 図が問題の図と少し形が異なりますね。 まぁ、気にしない。気にしない。