証明例 　

対偶の作戦でもとるか。

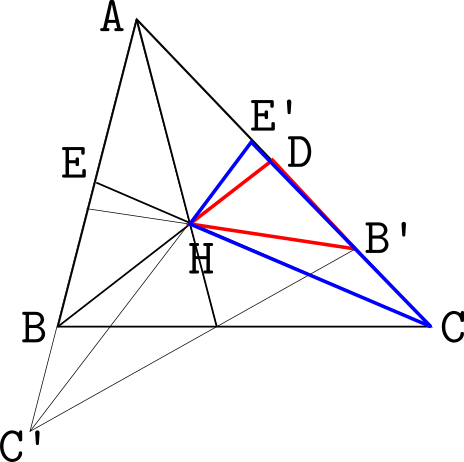
$BD$ と $CE$ の交点を$H$とする。

直線 $AH$ は $\angle A$ の二等分線。これを鏡映線として $\triangle ABC$ 他図形全体の鏡映をとる。

鏡映点の名前は対応点の名前に $'$ を付けたものとしておこう。 着目すべき3角形に色をつけてみた。

$\angle B \neq \angle C$ のとき、 図のように $\angle B \gt \angle C$ としてよい。

赤い三角形から、$BD = B'H + HD$

青い三角形から、$CE = CH + HE'$

であきらかに $CE \gt BD$。

つまり$\angle B \neq \angle C$ なら $CE \neq BD$

そして、$\angle B = \angle C$ なら$CE = BD$ はあきらか。

だから、逆をとってもいいし、対偶をとってもいいし。

---

[PS.]鏡映をとってみました。論理を使ってるから、中学生には酷かな。やってないはずはないけど。

ちなみに元の命題とその対偶命題とは真偽が一緒です。

逆を行く場合は、真偽はすぐには確定しません。でも排他的ですから、こちらも明らかです。

この間までの答え間違ってたからやり直し。あぁ恥ずかし。